【筆記】Link Cut Tree

引入

Link Cut Tree 是一種資料結構，能夠動態維護樹/森林的聯通性和一些路徑上的操作和查詢。

請你維護一些森林，並進行以下操作 (強制在線)：

  1. 修改 $u, v$ 路徑上的權值
  2. 查詢 $u, v$ 路徑上的權值和
  3. 在 $u, v$ 之間連邊 (保證連邊之前 $u, v$ 不連通)
  4. 斷開 $u, v$ 之間的邊

單看 1 和 2 的話就是輕重鏈剖分的模板題。現在加上了連邊和斷邊的操作，這部分是輕重鍊剖分無法快速維護的。話雖如此，我們可以沿用它的精神，重新定義樹鏈，並用不同的方式維護。

鏈的維護

在 Link Cut Tree 中，每一條邊的狀態是根據最後一次的操作決定的。假設最後一次操作節點 $v$，則我們會把 $root$ 到 $v$ 的路徑設為重鏈。因此，每個節點 $v$ 最多只有一條連向自己兒子的重邊。我們稱這條邊為 $v$ 的 preferred edge，連到的子孫為 $v$ 的 preferred child。每一條鏈我們都用一棵 Splay Tree 維護，具體的維護方式會在等下提到。

我們先來定義一些名詞：

  • 代表樹：原本的樹。
  • 輔助樹：維護鏈的 Splay Tree。
  • path parent：重鏈在代表樹中深度最小節點的父節點。
  • parent：節點在輔助樹中的父節點。

每棵輔助樹內部會按照節點在代表樹的深度 ($v$ 的深度為代表樹 $root$ 到 $v$ 的距離) 作為權值維護 Splay Tree。

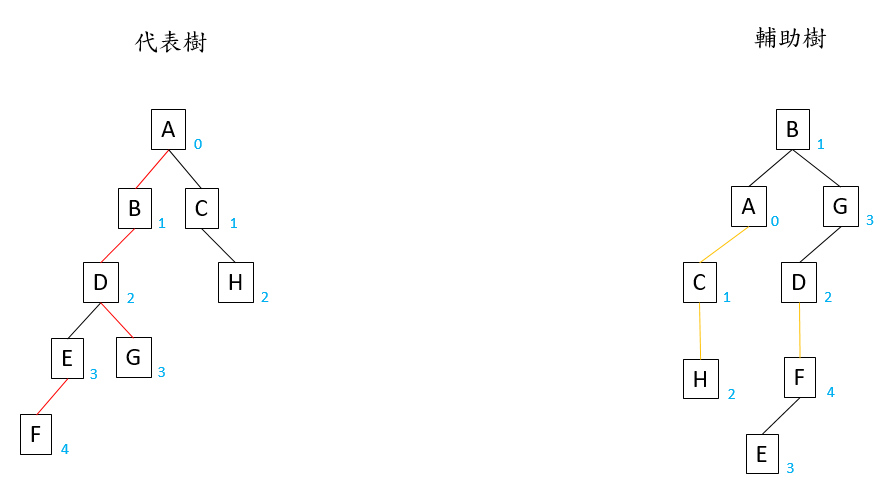
Link Cut Tree 範例

左圖中紅色的邊為重邊，藍色的數字為節點的深度。

右圖中由黑色的邊連起來的節點為一棵輔助樹。每一棵輔助樹滿足二元搜尋樹的性質。輔助樹之間被橘色的邊連起來，由輔助樹的 $root$ 連向 path parent。以 $EF$ 這條鏈來說，$E$ 是代表樹中深度最淺的點，path parent 為 $D$。因此 $EF$ 輔助樹的 $root$ $F$ 連向 $D$。

Splay Tree 中核心的操作為 splay()，把節點透過左旋和右旋移動到根結點，並保持二元搜尋樹的性質。splay() 操作的時間複雜度均攤為 $O(\log n)$。當我們在對 Splay Tree 旋轉的時候連向 path parent 的邊也要一起維護。

以下的程式碼為 Splay Tree 一些關鍵的函式。rev 變數為反轉的懶人標記。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
struct splay_node {
	splay_node* l = nullptr;
	splay_node* r = nullptr;
	splay_node* p = nullptr;
	bool rev = false;

	bool is_root() const { return p == nullptr || (p->l != this && p->r != this); }

	void push() {
		if(rev) {
			std::swap(l, r);
			if(l != nullptr) {
				l->rev ^= 1;
			}
			if(r != nullptr) {
				r->rev ^= 1;
			}
			rev = false;
		}
	}

	void rotate() {
		auto g = p->p;
		if(!p->is_root()) {
			(g->r == p ? g->r : g->l) = this;
		}
		p->push();
		push();
		if(p->l == this) {
			p->l = r;
			r = p;
			if(p->l != nullptr) {
				p->l->p = p;
			}
		} else {
			p->r = l;
			l = p;
			if(p->r != nullptr) {
				p->r->p = p;
			}
		}
		p->p = this;
		p = g;
	}

	void splay() {
		while (!is_root()) {
			auto g = p->p;
			if(!p->is_root()) {
				((g->r == p) == (p->r == this) ? p : this)->rotate();
			}
			rotate();
		}
		push();
	}
};

因為一棵輔助樹只有根結點需要存這條鏈的 path parent，程式碼中的變數 p 與 path parent 共用。is_root() 函式的實作方式也稍有不同，如果 p 沒有指向自己的話代表這個 p 是 path parent (右圖中橘色的邊)，否則是 Splay Tree 中的 parent (右圖中黑色的邊)。因此輔助樹的 $root$ 的 p 會有找不到自己兒子的情況。

access(v)：把 $v$ 到根結點的路徑設為重鏈。

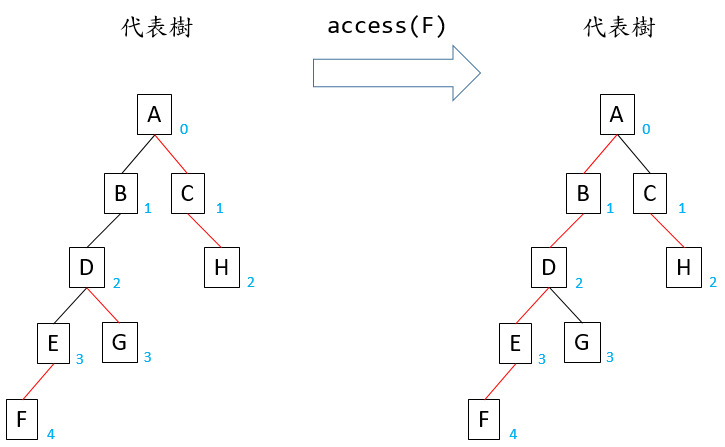
Access 函式示意圖

注意到 $C$ 和 $H$ 之間的重邊不會被斷開。

先對 $F$ 呼叫 splay() 旋轉到 $EF$ 輔助樹的樹根。因為 $F$ 是最後操作的節點，根據定義他沒有 preferred child，所以要把 $F$ 在輔助樹的右兒子斷開 (因為輔助樹按照節點在代表樹的深度維護，$F$ 在輔助樹中右子樹節點在代表樹中的深度都比 $F$ 深)。

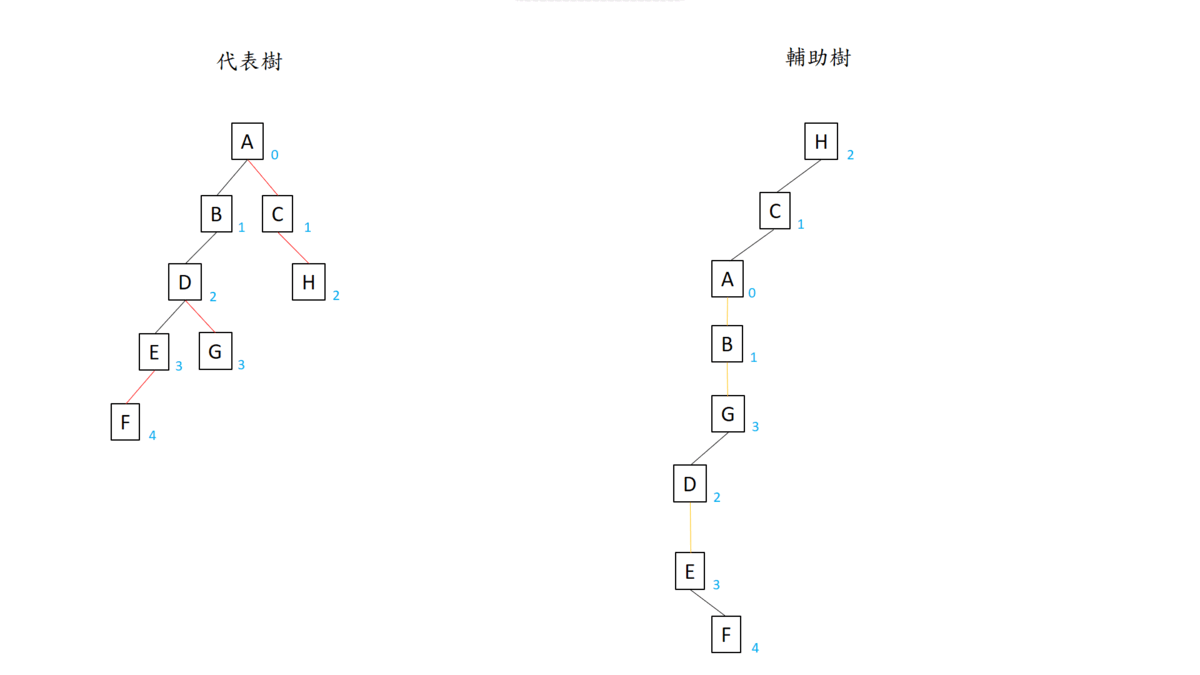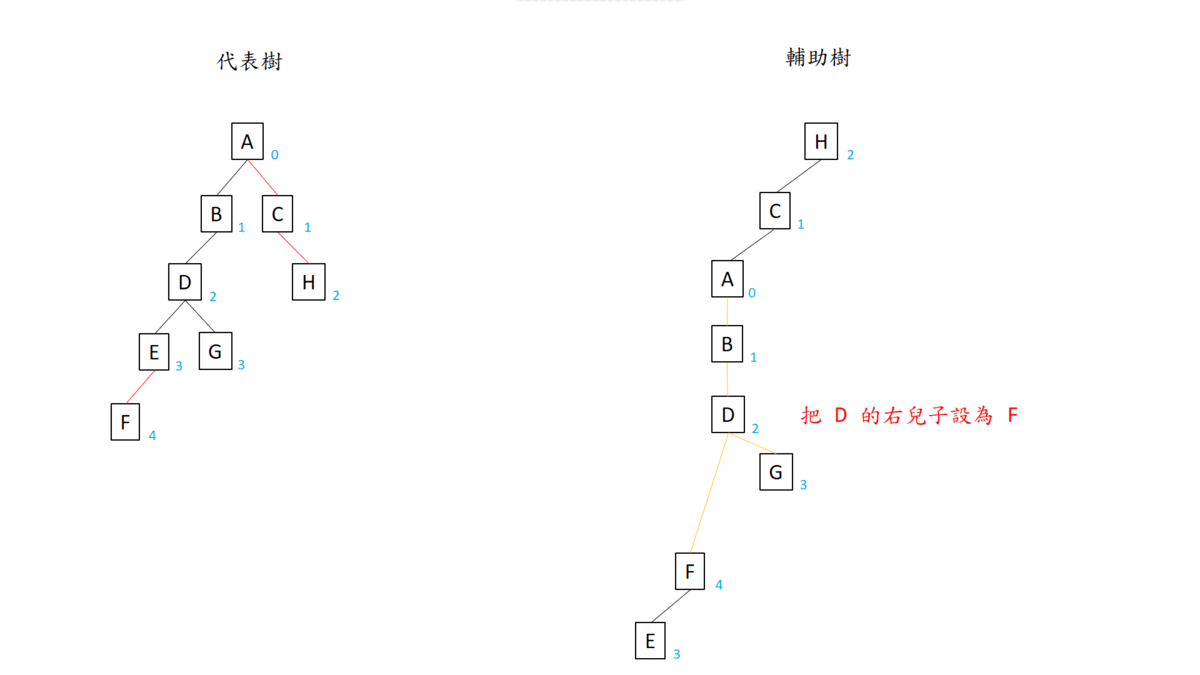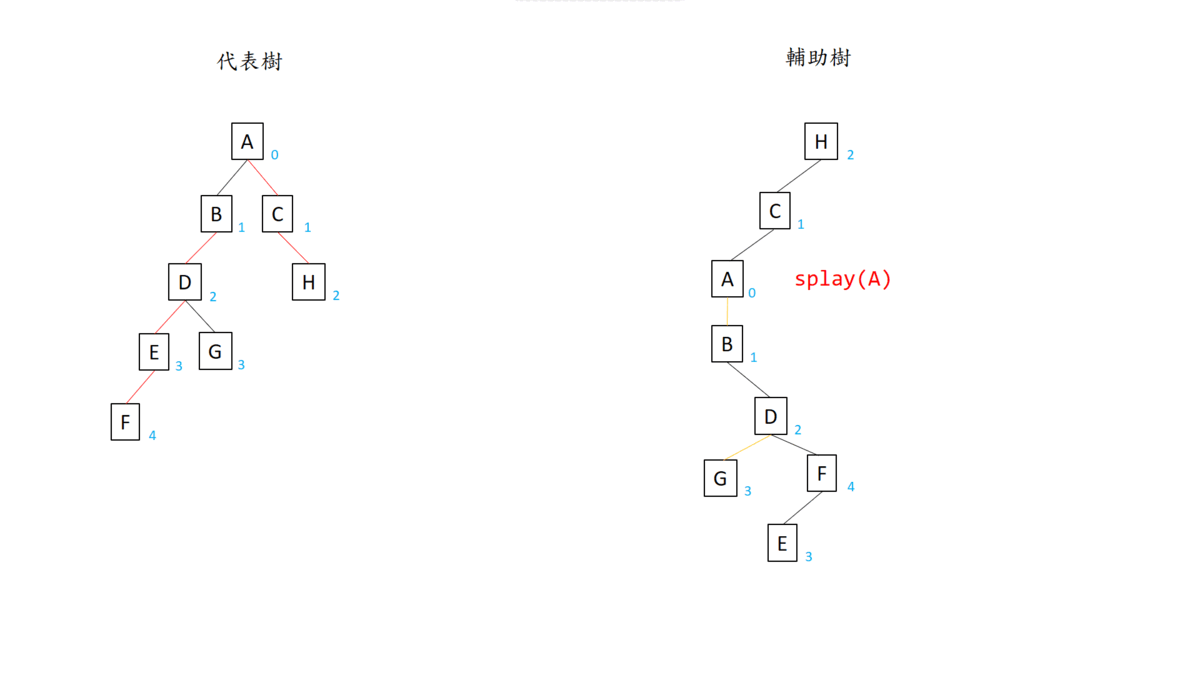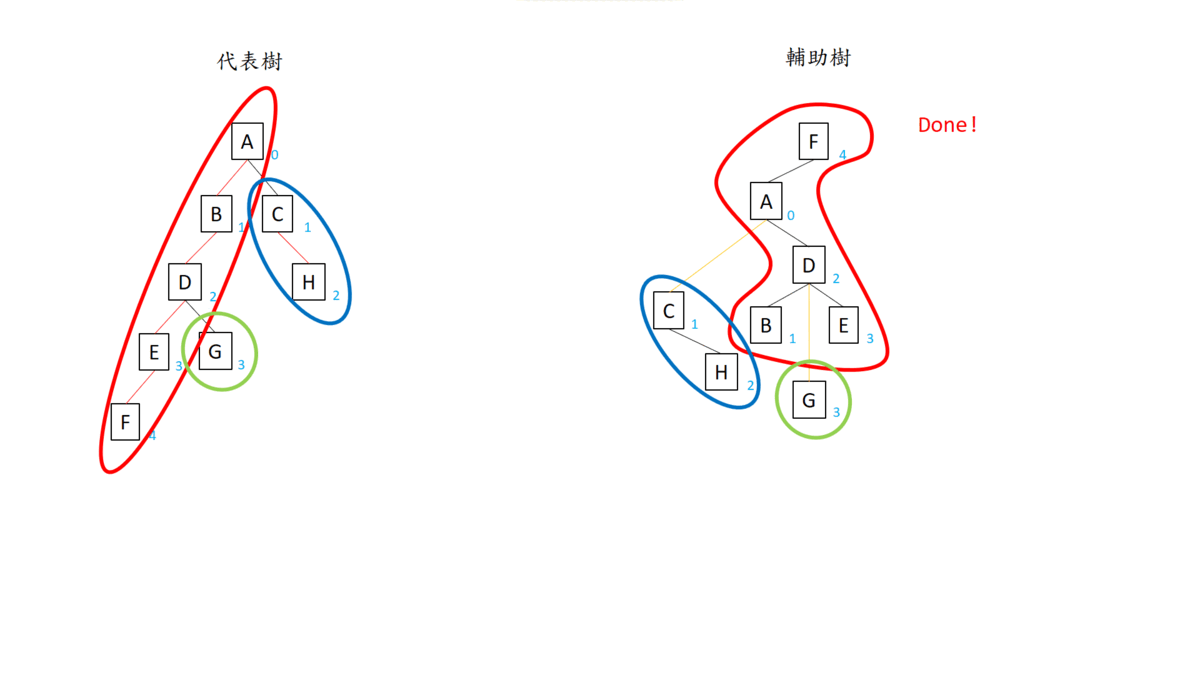
此時 $F$ 變成輔助樹的樹根，他的 path parent 是 $D$。我們要把 $D$ 的 preferred child 變成 $E$，相當於在輔助樹中將 $D$ 的右兒子設成 $E$ 所在的輔助樹的根結點 $F$。先把 $D$ splay() 到 $DG$ 輔助樹的樹根，然後把右兒子斷開並連到 $F$。這樣我們就成功合併兩棵輔助樹，相當於合併成一條重鏈，並且輔助樹維持二元搜尋樹的性質。

我們持續往上合併，直到重鏈連接到樹根。最後 $A$ 到 $F$ 形成一條重鏈，也就是他們在同一棵輔助樹中。最後我們再對 F 呼叫 splay()，讓 F 旋轉到輔助樹的樹根，此時 $F$ 沒有 parent。

Access 函式動畫

1
2
3
4
5
6
7
8
9
10
splay_node* access(splay_node* v) {
	splay_node* last = nullptr;
	for(splay_node* p = v; p != nullptr; p = p->p) {
		p->splay();
		p->r = last;
		last = p;
	}
	v->splay();
	return last;
}

有了 access(v) 的核心操作之後，剩下的操作就簡單很多了。

make_root(v)：把 $v$ 設定為代表樹中的樹根。

我們先呼叫 access(v)，讓根結點到 $v$ 成為一條鏈，此時 $v$ 是這條鏈中最深的節點，並且位於輔助樹的樹根。我們對 $v$ 打反轉的懶人標記，這樣 $v$ 就變成這條鏈中深度最淺的節點，也就變成樹根了！

1
2
3
4
void make_root(splay_node* v) {
	access(v);
	v->rev ^= 1;
}

link(u, v)：在 $u, v$ 之間連一條邊。

先呼叫 make_root(v)，讓 $v$ 變成他代表樹的根結點，接著直接把他的 path parent 設為 $u$。

1
2
3
4
void link(splay_node* u, splay_node* v) {
	make_root(v);
	v->p = u;
}

cut(u, v)：切斷連接 $u, v$ 的邊。

先呼叫 make_root(u)，讓 $u$ 變成代表樹的樹根。接著再呼叫 access(v)，讓 $u, v$ 形成一條長度為 $1$ 的重鏈，且因為 $v$ 是最後 access 的點，所以他位於輔助樹的樹根，左邊的兒子是 $u$。最後直接移除 $v$ 的左兒子，和把 $u$ 的 parent 設為 null ($u$ 的 parent 也要移除，否則只是讓 $v$ 變成 $u$ 的 path parent)。

1
2
3
4
5
6
void cut(splay_node* u, splay_node* v) {
	make_root(u);
	access(v);
	v->l->p = nullptr;
	v->l = nullptr;
}

is_connected(u, v)：回傳 $u, v$ 是否連通。

先呼叫 access(u)，讓根結點到 $u$ 成為一條鏈，且 $u$ 為這條鏈輔助樹的樹根，因此 $u$ 沒有 parent。這時候再呼叫 access(v)，這時候 $v$ 也沒有 parent。因為一棵代表樹中只有根結點所在的輔助樹樹根會沒有 parent。如果 $u$ 在 access(v) 後變成有 parent，就代表 $u, v$ 在同一棵代表樹上，也就是連通。

1
2
3
4
5
bool is_connected(splay_node* u, splay_node* v) {
	access(u);
	access(v);
	return u->p != nullptr;
}

優化 Dinic

我們可以使用 Link Cut Tree 來優化 Dinic，達到 $O(VE \log V)$ 的時間複雜度。有 $4$ 種操作可以用 Link Cut Tree 進行優化：

  1. 加邊：增廣時加邊直到 source 跟 sink 連通。
  2. 求路徑最小值：尋找增廣路徑中剩餘流量最小的邊。
  3. 路徑修改：把增廣路上的 capacity 全部減少增廣的流量
  4. 刪邊：刪掉 capacity 為 $0$ 的邊

以上 $4$ 種操作都能夠以 Link Cut Tree 維護。

雖然用 Link Cut Tree 的理論時間複雜度較優，但實際上因為常數頗大，除非範圍很大，否則執行時間不會比較快。

Exercises

References

競程 > 筆記
#Link Cut Tree
【筆記】Link Cut Tree
https://fffelix-huang.github.io/posts/link-cut-tree/
Author
老鼠
Posted on
July 19, 2023
Licensed under