【筆記】Slope Trick

介紹

Slope Trick 是一種表示某種特定函數的方式，該函數滿足：

1. 函數在座標平面上連續
2. 可以被分成多個區段，每個區段都是線性函數
3. 每個區段的斜率由左到右遞增或遞減，也就是凹或凸函數

我們稱它為 分段線性凸(凹)函數 (Slope Trickable Function)。

這個技巧可以被用來優化 DP。

表示法

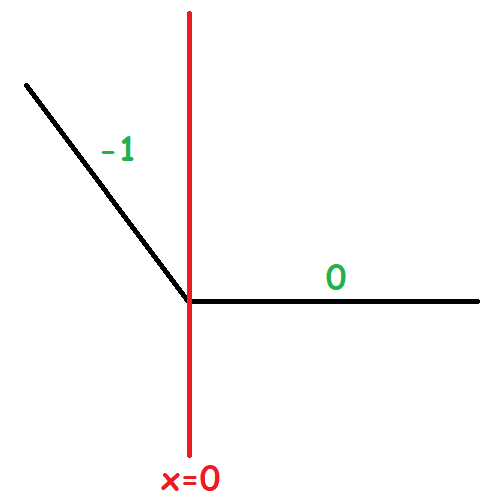
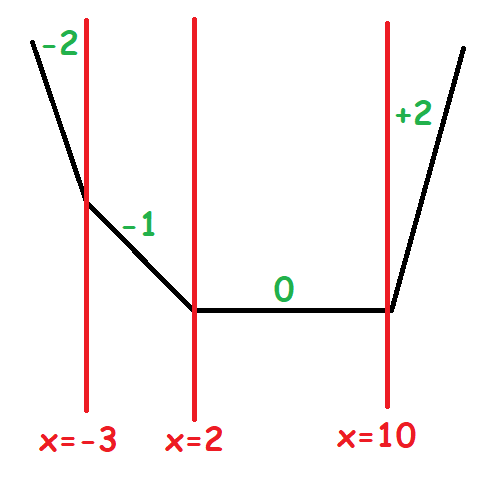
我們稱函數斜率改變的地方為分段點。紀錄分段點的 $x$ 座標，每次代表函數的斜率 $+1$。

分段點 = $[0]$	分段點 = $[-3, 2, 10, 10]$

性質

若兩個函數 $f(x), g(x)$ 為 Slope Trickable Function，且同時為凹(或凸)函數，則 $h(x) = f(x) + g(x)$ 也會是 Slope Trickable Function。同時，$h(x)$ 的分段點會是 $f(x)$ 和 $g(x)$ 分段點的聯集。

例題

CSES - Increasing Array II

給定長度為 $n$ 的數列 $a$，每次操作可以選擇數列中的一個數字 $a_i$，使其 $+1$ 或 $-1$。問使 $a$ 數列非嚴格遞增的最少操作次數？

• $1 \leq n \leq 2 \cdot 10^5$
• $1 \leq a_i \leq 10^9$

先從最基本的 $dp$ 下手。定義 $dp[i][j]$ 為使 $a_1, \dots, a_i$ 非嚴格遞增且 $a_i = j$ 的最少操作次數。我們可以列出 $dp$ 的轉移式：

\begin{cases}
dp[1][j] &= |a_1 - j| & \text{base case} \\
dp[i][j] &= \min\limits_{k \leq j} \{ dp[i - 1][k] + |a_i - j| \}, i > 1 & \text{轉移} \\
\end{cases}

由上述的轉移不難看出 $dp[i]$ 為 Slope Trickable Function。

最後的答案就是 $dp[n]$ 函數的最小值，也就是 $\min\limits_{j} dp[n][j]$

因為 $dp$ 為凸函數，函數的最小值會發生在斜率為 $0$ 的區段，這是我們想要維護的資訊。

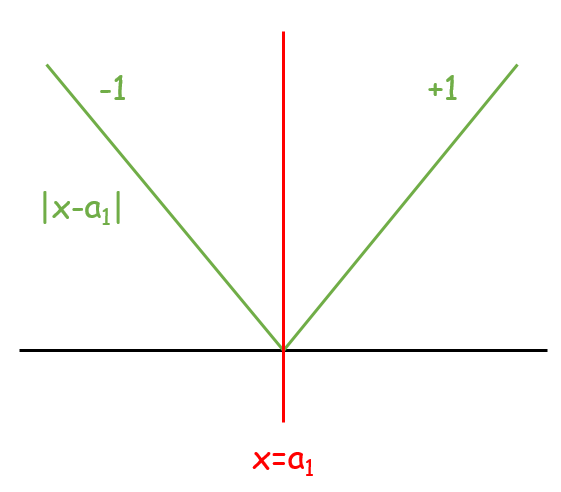
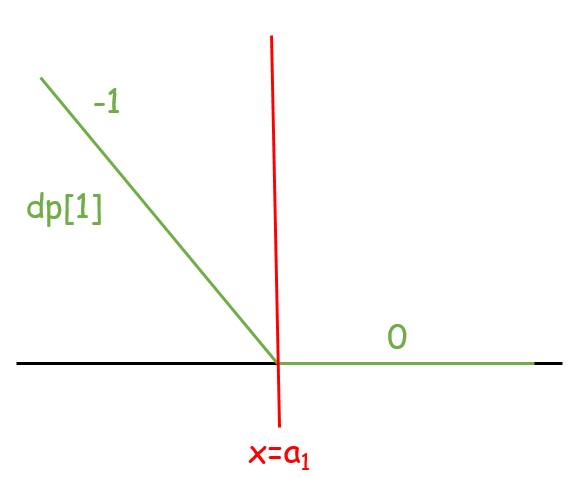
先從 base case 出發。可以發現 $|x - a_1|$ 函數在斜率 $> 0$ 的區段只會讓答案變得更差，並且使後續的數字更難滿足條件，因此我們可以把這個區段的斜率壓平成 $0$。

$|x - a_1|$ 函數圖形	把斜率 $> 0$ 的區段壓平

接下來我們來看如何從 $dp[i - 1]$ 轉移到 $dp[i]$。假設 $dp[i - 1]$ 最右邊的分段點為 $p$，分成兩種 case：

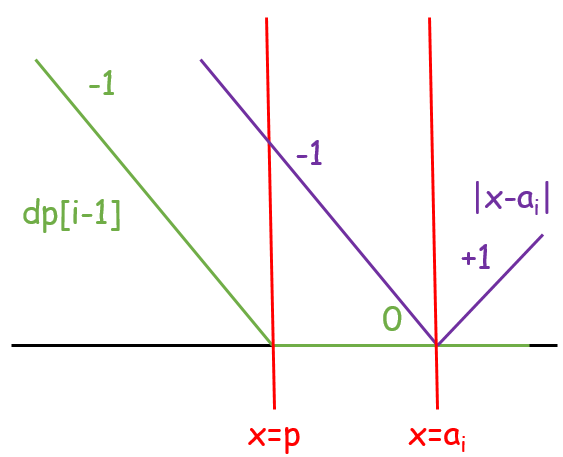
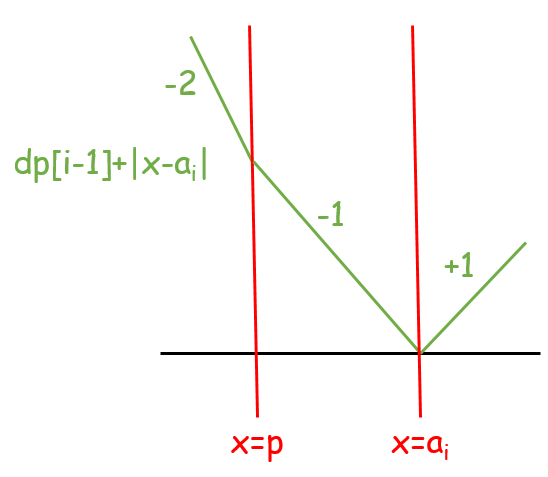
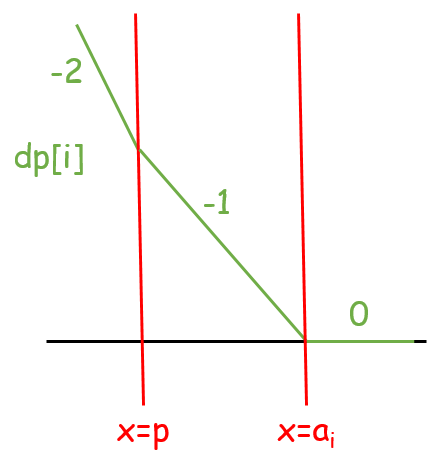
1. $p \leq a_i$：函數的最小值沒有改變，新增一個分段點在 $a_i$。

新增 $|x - a_i|$	合併函數	把斜率 $> 0$ 的區段壓平

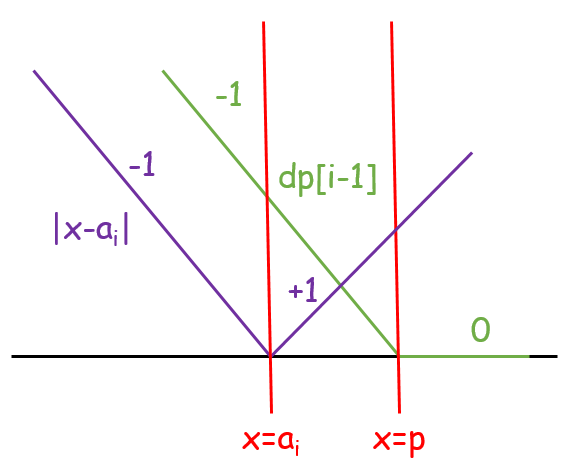
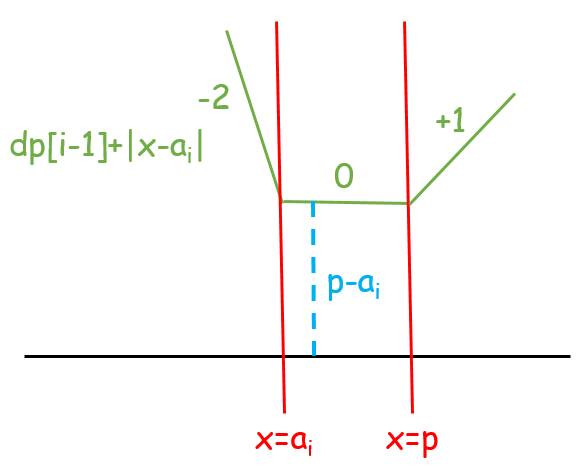
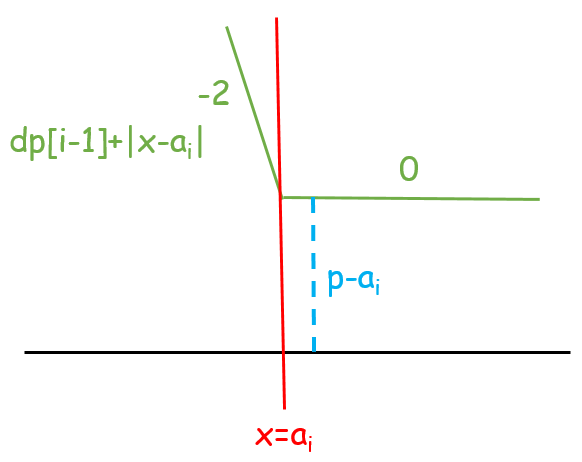
2. $p > a_i$：函數的最小值增加 $|p - a_i|$，移除 $p$ 的分段點，並在 $a_i$ 加入兩次分段點。

新增 $|x - a_i|$	合併函數，函數的最小值增加 $p - a_i$	把斜率 $> 0$ 的區段壓平

維護函數的分段點，並用一個變數紀錄斜率 $= 0$ 的高度即可。

Solution Code

#include <bits/stdc++.h>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	int n;
	cin >> n;
	priority_queue<int> pq;
	long long ans = 0;
	for(int i = 0; i < n; i++) {
		int x;
		cin >> x;
		if(pq.empty() || x > pq.top()) {
			pq.push(x);
		} else {
			ans += pq.top() - x;
			pq.pop();
			pq.push(x);
			pq.push(x);
		}
	}
	cout << ans << "\n";
	return 0;
}

Exercises

• CF 713C - Sonya and Problem Wihtout a Legend
• ARC070 E - NarrowRectangles

References

• https://codeforces.com/blog/entry/47094?#comment-315161
• maspypy - Slope Trick